A typical lawn sprinkler features various nozzles arranged at angles on a rotating wheel; when water is pumped in, they release jets that cause the wheel to rotate. But what would happen if the water were sucked into the sprinkler instead? In which direction would the wheel turn then, or would it even turn at all? That’s the essence of the “reverse sprinkler” problem that physicists like Richard Feynman, among others, have grappled with since the 1940s. Now, applied mathematicians at New York University think they’ve cracked the conundrum, per a recent paper published in the journal Physical Review Letters—and the answer challenges conventional wisdom on the matter.
“Our study solves the problem by combining precision lab experiments with mathematical modeling that explains how a reverse sprinkler operates,” said co-author Leif Ristroph of NYU’s Courant Institute. “We found that the reverse sprinkler spins in the ‘reverse’ or opposite direction when taking in water as it does when ejecting it, and the cause is subtle and surprising.”
Ristroph’s lab frequently addresses these kinds of colorful real-world puzzles. For instance, back in 2018, Ristroph and colleagues fine-tuned the recipe for the perfect bubble based on experiments with soapy thin films. (You want a circular wand with a 1.5-inch perimeter, and you should gently blow at a consistent 6.9 cm/s.) In 2021, the Ristroph lab looked into the formation processes underlying so-called “stone forests” common in certain regions of China and Madagascar. These pointed rock formations, like the famed Stone Forest in China’s Yunnan Province, are the result of solids dissolving into liquids in the presence of gravity, which produces natural convective flows.
In 2021, his lab built a working Tesla valve, in accordance with the inventor’s design, and measured the flow of water through the valve in both directions at various pressures. They found the water flowed about two times slower in the nonpreferred direction. And in 2022, Ristroph studied the surpassingly complex aerodynamics of what makes a good paper airplane—specifically what is needed for smooth gliding. They found that paper airplane aerodynamics differ substantially from conventional aircraft, which rely on airfoils to generate lift.
The reverse sprinkler problem is associated with Feynman because he popularized the concept, but it actually dates back to a chapter in Ernst Mach’s 1883 textbook The Science of Mechanics (Die Mechanik in Ihrer Entwicklung Historisch-Kritisch Dargerstellt). Mach’s thought experiment languished in relative obscurity until a group of Princeton University physicists began debating the issue in the 1940s.
Feynman was a graduate student there at the time and threw himself into the debate with gusto, even devising an experiment in the cyclotron laboratory to test his hypothesis. (In true Feynman fashion, that experiment culminated with the explosion of a glass carboy used in the apparatus because of the high internal pressure.)
One might intuit that a reverse sprinkler would work just like a regular sprinkler, merely played backward, so to speak. But the physics turns out to be more complicated. “The answer is perfectly clear at first sight,” Feynman wrote in Surely You’re Joking, Mr. Feynman (1985). “The trouble was, some guy would think it was perfectly clear [that the rotation would be] one way, and another guy would think it was perfectly clear the other way.”
Mach proposed that there would be no rotation with a reverse sprinkler: the reaction force on the nozzle as it sucks in water pulls the nozzle counter-clockwise, while the water flowing into the inside of the nozzle pushes it clockwise. The two forces cancel each other out in this steady-state scenario. Feynman’s own experiment showed a slight tremor when pressure was first applied to pump water through the nozzle, and then the sprinkler returned to its original position and remained still.
But others suggested that if the friction was low enough and the inflow rate high enough, a reverse sprinkler will start to turn in the opposite direction of an ordinary sprinkler, thanks to the formation of a vortex inside. As Philip Ball wrote at APS Physics, since Feynman’s efforts, “some experiments have shown steady reverse rotation, some showed only transient rotation, and some situations led to unsteady rotation that changed direction or proceeded in a direction that depended on the experimental geometry.”
Enter Leif Ristroph and colleagues, who built their own custom sprinkler that incorporated ultra-low-friction rotary bearings so their device could spin freely. They immersed their sprinkler in water and used a special apparatus to either pump water in or pull it out at carefully controlled flow rates. Particularly key to the experiment was the fact that their custom sprinkler let the team observe and measure how water flowed inside, outside, and through the device. Adding dyes and microparticles to the water and illuminating them with lasers helped capture the flows on high-speed video. They ran their experiments for several hours at a time, the better to precisely map the fluid-flow patterns.
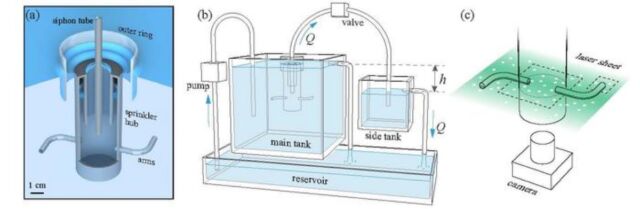
Ristroph et al. found that the reverse sprinkler rotates a good 50 times slower than a regular sprinkler, but it operates along similar mechanisms, which is surprising. “The regular or ‘forward’ sprinkler is similar to a rocket, since it propels itself by shooting out jets,” said Ristroph. “But the reverse sprinkler is mysterious since the water being sucked in doesn’t look at all like jets. We discovered that the secret is hidden inside the sprinkler, where there are indeed jets that explain the observed motions.”
A reverse sprinkler acts like an “inside-out rocket,” per Ristroph, and although the internal jets collide, they don’t do so head-on. “The jets aren’t directed exactly at the center because of distortion of the flow as it passes through the curved arm,” Ball wrote. “As the water flows around the bends in the arms, it is slung outward by centrifugal force, which gives rise to asymmetric flow profiles.” It’s admittedly a subtle effect, but their experimentally observed flow patterns are in excellent agreement with the group’s mathematical models.
Physical Review Letters, 2024. DOI: 10.1103/PhysRevLett.132.044003 (About DOIs).
Listing image by NYU’s Applied Mathematics Laboratory